Exercícios sobre plano cartesiano
Essa lista de exercícios vai testar seus conhecimentos sobre plano cartesiano e te auxiliar nos seus estudos de geometria analítica.
No plano cartesiano a seguir, estão demonstrados 4 pontos, um em cada quadrante:
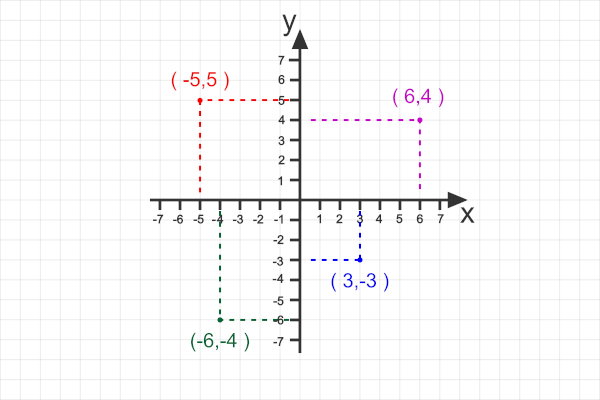
Analisando a imagem, podemos afirmar que o ponto sinalizado que pertence ao quarto quadrante é o ponto:
a) (6, 4)
b) (-5, 5)
c) (3, -3)
d) (-6, -4)
Para realizar um estudo de uma região de reserva florestal, o Instituto Brasileiro do Meio Ambiente (Ibama) decidiu colocar mais duas bases de observação em dois pontos diferentes dessa reserva. Sendo O(0,0) o dormitório, e A(30,50) e B(60,10) a localização das bases de observação, em km, a distância entre essas duas bases em km será de:
A) 40
B) 50
C) 60
D) 70
E) 80
Durante as aulas de robótica, um robô inicia em um ponto no plano cartesiano, na posição (2, 3). Ele se move 4 unidades para a direita e depois 5 unidades para baixo. Qual é a nova posição do robô?
A) (6, -2)
B) (2, -5)
C) (6, -1)
D) (8, 8)
Um gráfico no plano cartesiano mostra as vendas de um produto ao longo de vários meses. A equação da reta que melhor representa o crescimento das vendas é dada por y = 3x + 5, onde x representa o mês e y o número de unidades vendidas. Qual será o número de unidades vendidas no mês 7?
A) 21 unidades
B) 26 unidades
C) 33 unidades
D) 44 unidades
Duas escolas, a Escola Buriti e a Escola Pequi, estão localizadas nos pontos (10, 10) e (50, 40) em um mapa representado por um plano cartesiano. Para atender melhor à região, uma nova escola será construída exatamente no ponto médio entre as duas escolas existentes. Qual será a coordenada da nova escola?
A) (30, 25)
B) (20, 30)
C) (40, 25)
D) (30, 30)
E) (35, 20)
(Enem 2018) Para criar um logotipo, um profissional da área de design gráfico deseja construí-lo utilizando o conjunto de pontos do plano na forma de um triângulo, exatamente como mostra a imagem.
Para construir tal imagem utilizando uma ferramenta gráfica, será necessário escrever algebricamente o conjunto que representa os pontos desse gráfico.
Esse conjunto é dado pelos pares ordenados (x; y) ∈ N x N, tais que:
a) 0 ≤ x ≤ y ≤10
b) 0 ≤ y ≤ x ≤10
c) 0 ≤ x ≤ 10, 0 ≤ y ≤10
d) 0 ≤ x + y ≤10
e) 0 ≤ x + y ≤20
(Enem 2022) Uma pessoa precisa se deslocar de automóvel do ponto P para o ponto Q, indicados na figura, na qual as linhas verticais e horizontais simbolizam ruas.
Por causa do sentido de tráfego nessas ruas, o caminho poligonal destacado é a possibilidade mais curta de efetuar esse deslocamento. Para descrevê-lo, deve-se especificar qual o sentido a ser tomado em cada cruzamento de ruas, em relação à direção de deslocamento do automóvel, que se movimentará continuamente. Para isso, empregam-se as letras E, F e D para indicar
“vire à esquerda”, “siga em frente” e “vire à direita”, respectivamente.
A sequência de letras que descreve o caminho poligonal destacado é
a) DDEFDDEEFFD.
b) DFEFDDDEFFD.
c) DFEFDDEEFFD.
d) EFDFEEDDFFE.
e) EFDFEEEDFFE.
(Enem 2014) No Brasil há várias operadoras e planos de telefonia celular. Uma pessoa recebeu 5 propostas (A, B, C, D e E) de planos telefônicos. O valor mensal de cada plano está em função do tempo mensal das chamadas, conforme o gráfico.
Essa pessoa pretende gastar exatamente R$ 30,00 por mês com telefone.
Dos planos telefônicos apresentados, qual é o mais vantajoso, em tempo de chamada, para o gasto previsto para essa pessoa?
a) A
b) B
c) C
d) D
e) E
(Enem 2016) Uma família resolveu comprar um imóvel num bairro cujas ruas estão representadas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal. Desconsidere a largura das ruas.
A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A.
Com base nesses dados, o imóvel que atende às pretensões da família deverá ser localizado no encontro das ruas
a) 3 e C
b) 4 e C
c) 4 e D
d) 4 e E
e) 5 e C
O plano cartesiano é uma representação gráfica que organiza os pontos do plano de acordo com suas coordenadas. Ele é composto por dois eixos perpendiculares: o eixo horizontal, conhecido como eixo das abscissas, e o eixo vertical, chamado eixo das ordenadas. Esses eixos se cruzam no ponto de origem, formando quatro regiões chamadas de quadrantes. Considerando que um ponto P(a, b) tem as seguintes características: a < 0 e b > 0, a qual quadrante do plano cartesiano esse ponto pertence?
A) Primeiro quadrante
B) Segundo quadrante
C) Terceiro quadrante
D) Quarto quadrante
E) Eixo das ordenadas
Em um plano cartesiano foram marcados os pontos A (4, 5), B (-3, 2), C (-1, -4), D (2, -3), E (3, 1), F (-2, -1) e G (1, 3). O quadrante em que foram marcados mais pontos é:
A) I
B) II
C) III
D) IV
Sobre o plano cartesiano, julgue as afirmativas a seguir:
I - O eixo vertical é conhecido também como eixo das ordenadas.
II - O ponto B (4, -2) está localizado no quarto quadrante.
III - O eixo horizontal é conhecido também como eixo das coordenadas.
Podemos afirmar que:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas I e II são verdadeiras.
E) Somente as afirmativas II e III são verdadeiras.
Alternativa D
O quarto quadrante é o quadrante que possui valor de abscissa positivo e valor de ordenada negativo; no plano cartesiano demonstrado na imagem, o ponto que está no quarto quadrante é o ponto (3, -4).
Alternativa B
Calculando a distância entre os dois pontos temos que:
\(D_{AB} = \sqrt{30^2 + 40^2} \)
\(D_{AB} = \sqrt{900 + 1600} \)
\(D_{AB} = \sqrt{2500} \)
Alternativa A
Se ele está no ponto (2, 3) e se move 4 unidades para a direita, então 2 + 4 = 6; além disso, 5 unidades para baixo significam – 5, então temos que 3 – 5 = - 2. Portanto a localização desse ponto será (6, -2).
Alternativa B
Como sabemos que a equação que descreve a reta é y = 3x + 5, para saber o número de unidades vendidas no mês 7 basta substituir x = 7 na equação:
y = 3 ⋅ 7 + 5
y = 21 + 5
y = 26
Então, o número de unidades vendidas no mês 7 é de 26 unidades.
Alternativa A
Para calcular o ponto médio, temos que:
\(x_M = \frac{10 + 50}{2} = \frac{60}{2} = 30 \\ y_M = \frac{10 + 40}{2} = \frac{50}{2} = 25 \)
Então as coordenadas da escola nova serão (30, 25).
Alternativa B
Note que todos os pontos do plano cartesiano que estão na hipotenusa do triângulo são os pontos que possuem x = y, sendo os pontos (0,0); (1,1); (2,2); ... (10, 10). Perceba então que os valores de x e y estão sempre entre 0 e 10. Além disso, analisando o gráfico é possível verificar que os valores de y são sempre iguais ou menores que o valor de x, por exemplo, quando x = 10, temos os pontos (10, 10), (10, 9), (10, 8) ... (10, 0). Então y é sempre menor ou igual a x, logo podemos afirmar que:
0 ≤ y ≤ x ≤10
Alternativa C
Ao analisar o gráfico no plano cartesiano, o plano cujo tempo mensal em minutos é o maior possível para o valor de R$ 30,00 mensal é o plano C.
Alternativa C
Como o local de trabalho da mãe e o consultório do pai estão localizados na rua E, o imóvel precisa ser situado na rua 4, que é a linha de simetria entre os pontos correspondentes, garantindo que a distância até os dois locais seja a mesma. Sabemos que a distância do consultório até a escola é de 6 quarteirões, portanto o imóvel deve estar a 3 quarteirões de cada um desses lugares. Partindo da escola e caminhando 3 quarteirões pela rua 4, chegaremos à rua D.
O imóvel deverá ser posicionado no cruzamento da rua 4 com a rua D.
Alternativa B
Sabemos que no segundo quadrante os valores de abscissa são negativos e de ordenada são positivas, sendo assim P é um ponto do segundo quadrante.
Alternativa A
Vamos analisar a posição de cada ponto em relação aos quadrantes:
- Ponto A (4, 5): está no quadrante I, pois ambos os valores são positivos.
- Ponto B (-3, 2): está no quadrante II, pois o valor x é negativo e o valor y é positivo.
- Ponto C (-1, -4): está no quadrante III, pois ambos os valores são negativos.
- Ponto D (2, -3): está no quadrante IV, pois o valor x é positivo e o valor y é negativo.
- Ponto E (3, 1): está no quadrante I, pois ambos os valores são positivos.
- Ponto F (-2, -1): está no quadrante III, pois ambos os valores são negativos.
- Ponto G (1, 3): está no quadrante I, pois ambos os valores são positivos.
- Quadrante I: A, E, G (3 pontos)
- Quadrante II: B (1 ponto)
- Quadrante III: C, F (2 pontos)
- Quadrante IV: D (1 ponto)
Então, o quadrante com o maior número de pontos é o quadrante I.
Alternativa D
I - Verdadeira. No plano cartesiano, o eixo vertical é chamado de eixo das ordenadas.
II - Verdadeira. O ponto B tem coordenadas (4, -2). O primeiro valor é positivo (4), o que significa que está à direita do eixo y, e o segundo valor é negativo (-2), indicando que está abaixo do eixo x. Isso demonstra que o ponto está no quarto quadrante.
III - Falsa. O eixo horizontal é conhecido como eixo das abscissas, não "eixo das coordenadas".


